Tính chất đường phân giác trong tam giác và ví dụ bài tập

Bài viết lách tính hóa học lối phân giác vô tam giác gồm những: đặc điểm đường phân giác trong tam giác vuông, đặc điểm lối phân giác vô tam giác cân nặng, đặc điểm lối phân giác vô và ngoài của tam giác…

Định lí:

Bạn đang xem: Tính chất đường phân giác trong tam giác và ví dụ bài tập

* Đường phân giác vô của một tam giác phân chia cạnh đối lập trở thành nhì đoạn trực tiếp tỉ trọng với nhì cạnh kề với nhì đoạn ấy.

* Đường phân giác ngoài bên trên một đỉnh của tam giác phân chia cạnh đối lập trở thành nhì đoạn trực tiếp tỉ trọng với nhì cạnh kề với nhì đoạn trực tiếp ấy.

$\begin{array}{l}\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\\\frac{{EB}}{{EC}} = \frac{{AB}}{{AC}}\end{array}$

Tính hóa học lối phân giác vô tam giác

Như vậy, chân những lối phân giác vô và phân giác ngoài của một góc bên trên một đỉnh của tam giác là những điểm phân chia vô và phân chia ngoài cạnh đối lập theo gót tỉ số bởi vì tỉ số của nhì cạnh mặt mũi ứng.

$\frac{{DB}}{{DC}} = \frac{{EB}}{{EC}} = \frac{{AB}}{{AC}}.$

Tính hóa học lối phân giác của góc ngoài của tam giác

Định lí vẫn trúng với lối phân giác của góc ngoài của tam giác
Tính hóa học lối phân giác vô tam giác
Trong tam giác ABC sở hữu AD’ là tia phân giác góc ngoài đỉnh A thì $\frac{D'B}{D'C}=\frac{AB}{AC}\,\ (AB\neq AC)$

Ví dụ minh họa đặc điểm lối phân giác vô tam giác

Ví dụ 1: Cho tam giác ABC với AB = c, AC = b, BC = a. Kẻ tia phân giác AD của góc A.

1. Tính phỏng lâu năm những đoạn trực tiếp BD, CD.

2. Đường trực tiếp tuy nhiên song với AC, kẻ kể từ D, rời cạnh AB bên trên điểm E. Tính BE, AE và DE.

Lời giải:

1. Ta sở hữu, theo gót ấn định lí về đặc điểm của lối phân giác:

$\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}} \Rightarrow \frac{{DB}}{{DC}} = \frac{c}{b} \Rightarrow \frac{{DB}}{{DB + DC}} = \frac{c}{{b + c}}$

$\Rightarrow \frac{{DB}}{{BC}} = \frac{c}{{b + c}} \Rightarrow DB = \frac{{ac}}{{b + c}}.$

Tương tự động, tớ có: $DC = \frac{{ab}}{{b + c}}$
Tính hóa học lối phân giác vô tam giác
2. DE // AC mang đến ta:

$\frac{{BE}}{{BA}} = \frac{{BD}}{{BC}} \Rightarrow \frac{{BE}}{c} = \frac{c}{{b + c}}$

$\Rightarrow BE = \frac{{{c^2}}}{{b + c}}$

Tương tự động, tớ có: $AE = \frac{{bc}}{{b + c}}$

AD là phân giác góc A: $\widehat {{A_1}} = \widehat {{A_2}}$

DE//AC: $\widehat D = \widehat {{A_1}}$

$\Rightarrow \Delta AED$ cân nặng bên trên E mang đến tớ $DE = AE = \frac{{bc}}{{b + c}}$

Ví dụ 2: Cho tam giác ABC, kẻ tia phân giác AD. Trên tia đối của tia BA, lấy điểm E sao mang đến BE = BD và bên trên tia đối của tia CA, lấy điểm F sao mang đến CF = CD.

1. Chứng minh EF // BC.

2. Chứng minh ED là phân giác của góc BEF và FD là phân giác của góc CFE.

Lời giải:

Tính hóa học lối phân giác vô tam giác
1. AD là phân giác của góc A nên:

$\frac{{BD}}{{CD}} = \frac{{AB}}{{AC}}$

Theo fake thiết, BE = BD và CF = CD nên tớ được:

$\frac{{EB}}{{FC}} = \frac{{AB}}{{AC}} \Rightarrow \frac{{EB}}{{AB}} = \frac{{FC}}{{AC}}$

Theo ấn định lí Talet, tớ suy rời khỏi EF // BC.

Xem thêm: Vé máy bay đi Đà Lạt giá rẻ nhất

2. $\Delta DBE$ cân nặng $\Rightarrow \widehat {{E_1}} = \widehat {{D_1}}$

${\rm{EF}}//BC \Rightarrow \widehat {{D_1}} = \widehat {{E_2}} \Rightarrow \widehat {{E_1}} = \widehat {{E_2}}$

$\Rightarrow ED$ là tia phân giác của góc BEF.

Trường ăn ý còn sót lại, chứng tỏ tương tự động (hoặc rất có thể phán xét, D là gửi gắm điểm của những lối phân giác vô của tam giác AEF).

Ví dụ 3: Cho tam giác ABC và một điểm D nằm trong cạnh BC, biết $\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}.$ Chứng minh AD là phân giác của góc A.

Lời giải:

Tính hóa học lối phân giác vô tam giác
Kẻ phân giác AD’ của góc A. Theo ấn định lí về đặc điểm của tam giác, tớ có:

$\frac{{D'B}}{{D'C}} = \frac{{AB}}{{AC}}$

Giả thiết mang đến $\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}$

Vậy $\frac{{D'B}}{{D'C}} = \frac{{DB}}{{DC}} \Rightarrow \frac{{D'B}}{{D'C + D'B}} = \frac{{DB}}{{DB + DC}} \\\Rightarrow \frac{{D'B}}{{BC}} = \frac{{DB}}{{BC}}$

$\Rightarrow D'B = DB.$

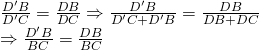
Vậy điểm D trùng với D’ hoặc AD là phân giác của góc A.

Ví dụ 4: Cho hình thoi ABCD. Trên tia đối của tia CD, lấy một điểm E, gọi F là gửi gắm điểm của AE và cạnh BC. Đường trực tiếp tuy nhiên song với AB kẻ qua chuyện F, rời đoạn trực tiếp BE bên trên điểm Phường. Chứng minh CP là phân giác của góc BCE.
Lời giải:
Tính hóa học lối phân giác vô tam giác
$AB//DE \Rightarrow \frac{{BF}}{{FC}} = \frac{{AB}}{{CE}}$

Mà AB = BC nên $\frac{{BF}}{{FC}} = \frac{{BC}}{{CE}}\,\,\,\,(1)$

FP // CE $\Rightarrow \frac{{BF}}{{FC}} = \frac{{PB}}{{PE}}\,\,\,\,\,(2)$

Từ (1) và (2) suy rời khỏi $\frac{{PB}}{{PE}} = \frac{{CB}}{{CE}} \Rightarrow$ CP là tia phân giác góc BCE.

Ví dụ 5: Cho hình bình hành ABCD. Phân giác của góc A rời lối chéo cánh BD bên trên E và phân giác của góc B rời lối chéo cánh AC bên trên F. Chứng minh EF // AB.
Lời giải:
Tính hóa học lối phân giác vô tam giác
Ta sở hữu $\frac{{ED}}{{EB}} = \frac{{ED}}{{AB}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)$

$\frac{{FC}}{{FA}} = \frac{{BC}}{{AB}} = \frac{{AD}}{{AB}}\,\,\,\,\,\,\,\,\,(2)$

Từ (1) và (2) suy rời khỏi $\frac{{ED}}{{EB}} = \frac{{FC}}{{FA}}$

Gọi O là gửi gắm điểm của hai tuyến đường chéo cánh, tớ có:

$\frac{{ED}}{{EB}} = \frac{{FC}}{{FA}} \Rightarrow \frac{{ED}}{{EB - ED}} = \frac{{FC}}{{FA - FC}}$ $\Rightarrow \frac{{ED}}{{OE}} = \frac{{FC}}{{OF}}$

$\Rightarrow {\rm{EF//DC}}$

Ví dụ 6: Cho tam giác ABC, sở hữu cạnh BC cố định và thắt chặt, đỉnh A thay cho thay đổi tuy nhiên tỉ số $\frac{{AB}}{{AC}} = k,$ với k là một trong những thực dương mang đến trước. Các tia phân giác vô và ngoài bên trên đỉnh A, rời cạnh BC và rời đường thẳng liền mạch BC theo gót trật tự bên trên những điểm D, E.

1. Chứng minh rằng D, E là nhì điểm cố định và thắt chặt.

2. Tìm quỹ tích đỉnh A.

Lời giải:
Tính hóa học lối phân giác vô tam giác

1. Theo ấn định lí về đặc điểm của lối phân giác, tớ có:

$\begin{array}{l}\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}} = k\\\frac{{EB}}{{EC}} = \frac{{AB}}{{AC}} = k.\end{array}$

Các tỉ số $\frac{{DB}}{{DC}}$ và $\frac{{EB}}{{EC}}$ bởi vì k ko thay đổi, nhì điểm B, C cố định và thắt chặt, suy rời khỏi nhì điểm D, E phân chia vô và phân chia ngoài đoạn trực tiếp cố định và thắt chặt BC theo gót một tỉ số ko thay đổi nên D và E là nhì điểm cố định và thắt chặt.

Xem thêm: Vé xem nhóm nhạc BlackPink biểu diễn tại Việt Nam là bao nhiêu?

2. AD và AE là những tia phân giác của nhì góc kề bù, vậy:

$AD \bot AE \Rightarrow \widehat {DAE} = {90^0}$

Điểm A nom đoạn trực tiếp cố định và thắt chặt DE bên dưới một góc vuông. Vậy quỹ tích A là lối tròn trặn 2 lần bán kính DE (có tâm là trung điểm I của DE và nửa đường kính $\frac{{DE}}{2}$ ).
Sotayhoctap chúc chúng ta học tập tốt!