Lý thuyết hai đường thẳng vuông góc

1. Tích vô vị trí hướng của nhì vectơ vô không khí.

- Góc thân thiết nhì véctơ vô ko gian:

Bạn đang xem: Lý thuyết hai đường thẳng vuông góc | SGK Toán lớp 11

Góc thân thiết nhì vectơ (khác véctơ không) $\vec{u},\vec{v}$ là góc $\widehat {BAC}$ với $\vec{AB}=\vec{u}$; $\vec{AC}=\vec{v}$

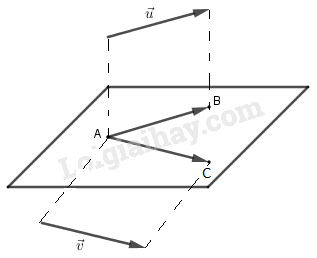
- Tích vô vị trí hướng của nhì vectơ vô ko gian:

Cho nhì vectơ không giống vectơ không $\vec{u},\vec{v}$ :

Biểu thức $\vec{u}.\vec{v}=|\vec{u}|.|\vec{v}|.cos(\vec{u},\vec{v})$ được gọi là tích vô vị trí hướng của nhì vectơ $\vec{u}$ và $\vec{v}$

Nếu $\vec{u}$ = $\vec{0}$ hoặc $\vec{v}$ = $\vec{0}$ thì tớ quy ước $\vec{u}$ . $\vec{v}$ = $\vec{0}$.

2. Vectơ chỉ phương của đường thẳng liền mạch.

- Vectơ $\vec{a} \ne \vec{0} $ là véctơ chỉ phương của đường thẳng liền mạch $d$ nếu như giá chỉ của $\vec{a}$ tuy nhiên song hoặc trùng với $d$.

- Nếu $\vec{a}$ là vectơ chỉ phương của đường thẳng liền mạch $d$ thì k$\vec{a}$ ($k ≠ 0$) cũng chính là vectơ chỉ phương của d.

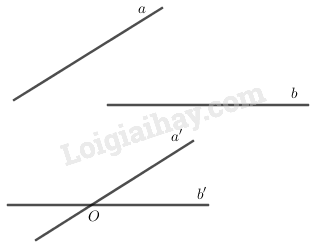
3. Góc thân thiết hai tuyến đường trực tiếp vô không khí.

Định nghĩa:

Góc thân thiết hai tuyến đường trực tiếp $a$ và $b$ vô không khí là góc thân thiết hai tuyến đường trực tiếp $a'$ và $b'$ nằm trong trải qua một điểm và thứu tự tuy nhiên song với $a$ và $b$

Nhận xét:

- Ta rất có thể lấy điểm $O$ nằm trong 1 trong những hai tuyến đường trực tiếp $a$ và $b$, rồi vẽ một đường thẳng liền mạch qua loa $O$ và tuy nhiên song với đường thẳng liền mạch sót lại.

- Nếu $\vec{u_{1}},\vec{u_{2}}$ thứu tự là vectơ chỉ phương của $a$ và $b$ và ($\vec{u_{1}},\vec{u_{2}}) = α$ thì:

+ góc $(a; b) = α$ nếu $0^0 ≤ α ≤ 90^0$

+ góc $(a; b) = 180^0- α$ nếu như $ 90^0 < α ≤ 180^0$.

- Nếu $a//b$ hoặc $a \equiv b$ thì $\widehat {\left( {a,b} \right)} = {0^0}$

Xem thêm: Mua cổ phiếu mấy ngày được bán? Cách bán ngay trong ngày giao dịch

4. Hai đường thẳng liền mạch vuông góc cùng nhau.

a) Định nghĩa:

Hai đường thẳng liền mạch được gọi là vuông góc cùng nhau nếu như góc thân thiết bọn chúng vày $90^0$

b) Nhận xét:

- Nếu$\vec{u_{1}},\vec{u_{2}}$ thứu tự là những VTCP của $a$ và $b$ thì: $a ⊥ b ⇔ \vec{u_{1}}.\vec{u_{2}}= 0$.

- Nếu $\left\{ \begin{array}{l}
a\, //b \, \\
c\, \bot \, a
\end{array} \right.$ thì $ c\, \bot \, b$

- Hai đường thẳng liền mạch vuông góc cùng nhau rất có thể rời nhau hoặc chéo cánh nhau.

c) Một số dạng toán thông thường gặp

Dạng 1: Tính góc thân thiết hai tuyến đường trực tiếp.

Phương pháp 1: Sử dụng tấp tểnh lý hàm số cô sin hoặc tỉ con số giác.

$\cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}$

Phương pháp 2: Sử dụng công thức tính cô sin góc thân thiết hai tuyến đường trực tiếp biết nhì véc tơ chỉ phương của bọn chúng.

$\cos \varphi = \left| {\cos \left( {\overrightarrow u ,\overrightarrow v } \right)} \right| = \dfrac{{\left| {\overrightarrow u .\overrightarrow v } \right|}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|}}$

Để tính $\overrightarrow u ,\overrightarrow v ,\left| {\overrightarrow u } \right|,\left| {\overrightarrow v } \right|$ tớ lựa chọn tía véc tơ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c $ ko đồng phẳng phiu tuy nhiên rất có thể tính được phỏng nhiều năm và góc thân thiết bọn chúng, tiếp sau đó biểu thị những véc tơ $\overrightarrow u ,\overrightarrow v $ qua loa những véc tơ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c $ rồi triển khai những đo lường và tính toán.

Dạng 2: Chứng minh hai tuyến đường trực tiếp vuông góc.

Phương pháp:

Để minh chứng hai tuyến đường trực tiếp ${d_1},{d_2}$ vuông góc tớ triển khai một trong những cách:

Xem thêm: Cách tải máy tính Casio 580 về điện thoại giúp bạn tính toán mọi lúc mọi nơi

Cách 1: Chứng minh $\overrightarrow {{u_1}} .\overrightarrow {{u_2}} = 0$, vô bại liệt $\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} $ là những VTCP của ${d_1},{d_2}$.

Cách 2: Sử dụng đặc thù $\left\{ \begin{array}{l}b//c\\a \bot c\end{array} \right. \Rightarrow a \bot b$

Cách 3: Sử dụng tấp tểnh lý Pi-ta-go hoặc xác lập góc thân thiết ${d_1},{d_2}$ và tính thẳng góc bại liệt.