1.Kiến thức chú ý về bất đẳng thức Cosi (Cauchy )
Bất đẳng thức Cauchy là 1 trong mỗi bất đẳng thức cần thiết và đem phần mềm rộng thoải mái nhập toán học tập. Được gọi là theo dõi căn nhà toán học tập người Pháp Augustin Louis Cauchy, bất đẳng thức cosi lớp 9 này hỗ trợ một cách thức hiệu suất cao nhằm ước tính độ quý hiếm khoảng của những thành phầm của những số thực.
Bất đẳng thức Cosi đem dạng:
Bạn đang xem: Chia Sẻ Công thức Bất Đẳng Thức Cosi lớp 9 - NIKKO
(a₁b₁ + a₂b₂ + … + aₙbₙ) ≤ √(a₁² + a₂² + … + aₙ²) √(b₁² + b₂² + … + bₙ²)
Trong tê liệt a₁, a₂, …, aₙ và b₁, b₂, …, bₙ là những số thực.
Để minh chứng bất đẳng thức Cosi, tớ dùng quyết định lí Pythagoras. Định lí Pythagoras xác minh rằng so với ngẫu nhiên tam giác vuông, tổng bình phương của 2 cạnh góc nhọn tiếp tục vày bình phương của cạnh huyền.
Áp dụng quyết định lí Pythagoras nhập bất đẳng thức cosi lớp 9, tớ có:
(a₁b₁ + a₂b₂ + … + aₙbₙ)² ≤ (a₁² + a₂² + … + aₙ²) (b₁² + b₂² + … + bₙ²)
Để minh chứng bất đẳng thức này, tớ cần thiết minh chứng rằng:
(a₁b₁ + a₂b₂ + … + aₙbₙ)² – (a₁² + a₂² + … + aₙ²) (b₁² + b₂² + … + bₙ²) ≤ 0
Bằng cơ hội bố trí những bộ phận ứng, tớ có:
[(a₁b₁)² – (a₁²)(b₁²)] + [(a₂b₂)² – (a₂²)(b₂²)] + … + [(aₙbₙ)² – (aₙ²)(bₙ²)] ≤ 0
Sử dụng đặc điểm của những số thực và bất đẳng thức AM – GM (bất đẳng thức thân thiện khoảng nằm trong và khoảng nhân), tớ rất có thể minh chứng rằng từng bộ phận nhập ngoặc đơn luôn luôn nhỏ rộng lớn hoặc vày 0.
Vì vậy, tớ Kết luận rằng bất đẳng thức Cosi là trúng và rất có thể vận dụng trong không ít vấn đề và cách thức đo lường và tính toán nhập toán học tập.

Giờ học tập toán bên trên trường
2.Một số vấn đề cần ghi nhớ về bất đẳng thức Cauchy
Định nghĩa: Bất đẳng thức Cauchy cho thấy rằng tổng của tích của những thành phần ứng kể từ nhị sản phẩm số thực ko vượt lên trước quá tích của tổng bình phương của từng sản phẩm số tê liệt.
Sử dụng nhập nhiều chủng loại bài bác toán: bất đẳng thức cosi lớp 9 rất có thể được dùng nhằm minh chứng những bất đẳng thức không giống, xử lý những vấn đề về lần độ quý hiếm lớn số 1 hoặc nhỏ nhất của một biểu thức.
Chứng minh: Bất đẳng thức Cauchy rất có thể được minh chứng bằng phương pháp dùng phép tắc chuyển đổi Cauchy-Schwarz, một nghệ thuật cần thiết nhập lý thuyết đại số và phân tách.
Ứng dụng: bất đẳng thức cosi lớp 9 được dùng nhập thật nhiều nghành nghề, kể từ toán học tập cơ bạn dạng cho tới những nghành nghề như toán học tập phần mềm, vật lý cơ, tài chính và tổng hợp.
Tóm lại, bất đẳng thức Cauchy là 1 khí cụ mạnh mẽ và uy lực và cần thiết nhập toán học tập, hỗ trợ một cách thức hiệu suất cao nhằm ước tính và đối chiếu những độ quý hiếm của những sản phẩm số thực.

Học sinh ôn lại bài bác tập
Bất đẳng thức cosine (còn được gọi là bất đẳng thức cao học tập, hoặc bất đẳng thức AM-GM cho tới hàm cosine) là 1 trong mỗi bất đẳng thức cosi lớp 9 cần thiết nhập toán học tập và có rất nhiều dạng trở nên thể không giống nhau. Bất đẳng thức này thông thường được dùng nhằm ước tính những biểu thức tương quan cho tới cosin, tuy nhiên là 1 trong mỗi hàm toán học tập cần thiết nhập hình học tập và phân tách.
Dưới đấy là một vài dạng của bất đẳng thức cosine phổ biến:
Dạng bài bác tập dượt về bất đẳng thức Cosi
Như vậy, những em vẫn cầm được những kỹ năng tương quan cho tới BĐT Cosi rồi đúng không nào này, lúc này hãy vận dụng bọn chúng nhằm lên đường giải một vài dạng bài bác tập dượt tuy nhiên freetuts vẫn liệt kê ngay lập tức sau đây nha:
Dạng 1: sát dụng thẳng BĐT Côsi nhập bài bác tập dượt minh chứng bất đẳng thức
Ví dụ: Cho 2 số dương a, b thỏa mãn nhu cầu a^2 + b^2 = 2, hãy bệnh minh:
(a/b + b/a)(a/b^2 + b/a^2) ≥ 4
Lời giải:
Vì a, b > 0 nên suy rời khỏi a/b > 0, b/a > 0, a/b^2 > 0, b/a^2 >0.
Áp dụng bdt Cosi, tớ có:
a/b + b/a ≥2 căn bậc nhị (a/b x b/a) = 2
a/b^2 + b/a^2 ≥2 căn bậc nhị (a/b^2 + b/a^2 ) = 2/(căn bậc 2(a x b)
Suy ra:
(a/b + b/a)(a/b^2 + b/a^2) ≥ 4/(căn bậc 2 của a x b) (1)
Mà tớ có:
Xem thêm: "Nơi giấc mơ tìm về" tập cuối lên sóng tháng 7: Mai Anh thay đổi sau biến cố lớn
2 = a^2 + b^2 ≥ 2 x (căn bậc 2 của a^2 x b^2) = 2.a.b
⇒ a.b ≤ 1 (2)
Kết hợp ý (1) và (2), tớ có:
(a/b + b/a)(a/b^2 + b/a^2) ≥ 4 (điều nên bệnh minh),
Dấu “=” xẩy ra Khi a = b = 1.
Dạng 2: Kỹ thuật thêm thắt hạn chế nhập bất đẳng thức cosi lớp 9
Đối với dạng toán này, những em hãy chuyển đổi BĐT rất cần phải bệnh bản thân bằng phương pháp nhân, phân tách hoặc thêm thắt hạn chế một vài, nhằm rất có thể đơn giản và giản dị được BĐT lúc đầu.
Lưu ý: Khi tách và vận dụng BDT cosi, nên phụ thuộc việc đáp ứng cho tới lốt “=” xẩy ra.
Ví dụ: Cho a, b là số thực dương, sao cho tới a > b, minh chứng rằng:
a + 1/(b.(a – b) ≥ 3.
Lời giải:
Coi 1/(b.(a – b), b, (a – b) là 3 số dương, ap dụng bất đẳng thức Co si cho tới 3 số dương tớ có:
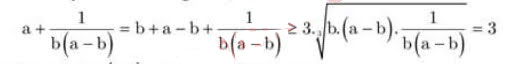
Dấu vày xẩy ra, Khi và chỉ khi:
a – b = b = 1/(b.(a – b) ⇔ a = 2; b = 1.
Dạng 3: Tìm độ quý hiếm lớn số 1, bé bỏng nhất của biểu thức
Ví dụ: Bài tập dượt lần GTLN, GTNN vày bất đẳng thức Cosi lớp 9
Cho nhị số dương a, b. Tìm độ quý hiếm lớn số 1 (GTLN) hoặc độ quý hiếm nhỏ nhất (GTNN) của những biểu thức nhập tình huống sau:
a. a + b = 8, lần GTLN của A = (a + b ).a.b
b. a.b = 6 ko thay đổi, lần GTNN của biểu thức B = (a + b)/ (a^2.b^2)
Lời giải:
Vì a + b = 8 nên tớ đem A = (a + b ).a.b = 8ab.
Áp dụng hệ trái ngược bất đẳng thức cô si, tớ có:
A đạt GTLN Khi và chỉ Khi (a x b) max ⇔ a = b (1)
Ta có: a + b = 8, a = b ⇒ a = b = 4.
Vậy A max = 6.4.4 = 96.
Vậy A đạt độ quý hiếm lớn số 1 là 96 Khi a = b = 4.
b. Ta đem B = (a + b)/ (a^2.b^2) = (a + b)/9^2 = (a + b)/81 vì như thế a.b = 9 luôn luôn ko thay đổi.
Áp dụng hệ trái ngược BĐT cosi, tớ có:
B min ⇔ (a + b) min ⇔ a = b.
Lúc này tớ có: a = b; a.b = 9 ⇒ a = b = 3.
Vậy B min = (3 + 3)/81 = 2/27
Vậy độ quý hiếm nhỏ nhất của B là 2/27 Khi a = 3 = 3.
Xem thêm: Lịch mở bán vé tàu Tết 2024 Giáp Thìn
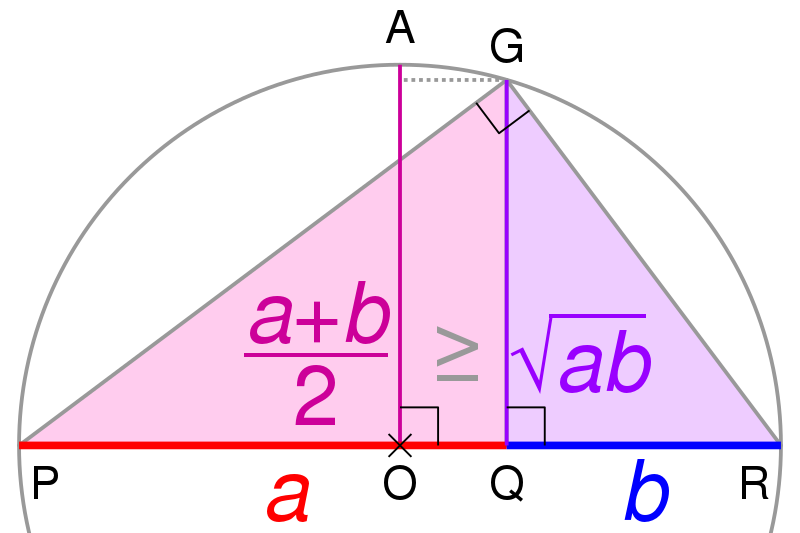
Bất đẳng thức Cosi
Bất đẳng thức cao học tập cơ bản: Đây là dạng cơ bạn dạng của bất đẳng thức cosi lớp 9, được biểu diễn
Những dạng của bất đẳng thức cosine này thông thường được dùng rộng thoải mái trong không ít nghành nghề của toán học tập, kể từ hình học tập cho tới phân tách và những yếu tố tương quan cho tới tối ưu hóa và ước tính. Đồng thời, bọn chúng cũng chính là khí cụ hữu ích nhập giải những vấn đề và bài bác tập dượt toán học tập.







Bình luận